Research

Challenge to establish modeling principles

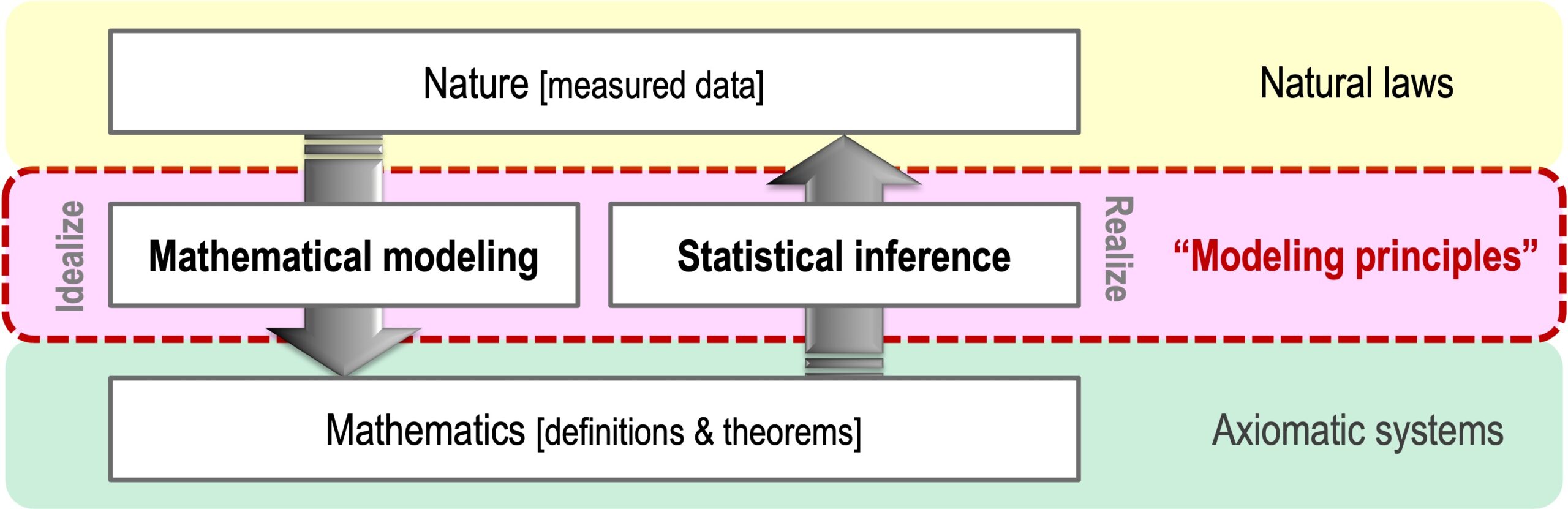
Our laboratory promotes theoretical and empirical research to establish guiding principles for unambiguously understanding all physical phenomena through mathematical modeling and statistical inference. Nature and mathematics stand alone under distinct rules, i.e., natural laws and axiomatic systems. Mathematical modeling is a way to connect these worlds, representing measured data using simple mathematical expressions. It establishes a foothold for understanding phenomena by separating their universal and individual aspects. However, models are idealized representations of parts of nature, allowing them to be handled mathematically, and are never a representation of the real nature itself. Statistical inference is a way to bring models closer to reality, enabling the selection of a more realistic model from among various candidates and the estimation of its parameters through quantitative matching with measured data. The combination of mathematical modeling and statistical inference allows two-way communication between nature and mathematics, i.e., between reality and the ideal.

Compared to the elaborate theoretical systems of mathematics, the guiding principles of mathematical modeling are not well-defined (i.e., not axiomatized), and this ambiguity can lead to controversy when interpreting phenomena. In addition, the statistical formulation and quantification of the “X-grounded validity” (where X represents discipline, such as physics, chemistry, biology, etc.) are required, as statistical inference does not always yield results that accurately reflect design philosophies of mathematical modeling in each discipline. We aim to establish unified rules that span mathematical modeling and statistical inference, which we refer to as “modeling principles,” and to build a discipline that consistently achieves the following two complementary approaches.

1. Mathematical modeling with the view toward statistical inference
2. Statistical inference reflecting design philosophies of mathematical modeling

Topic 1: Model indefiniteness

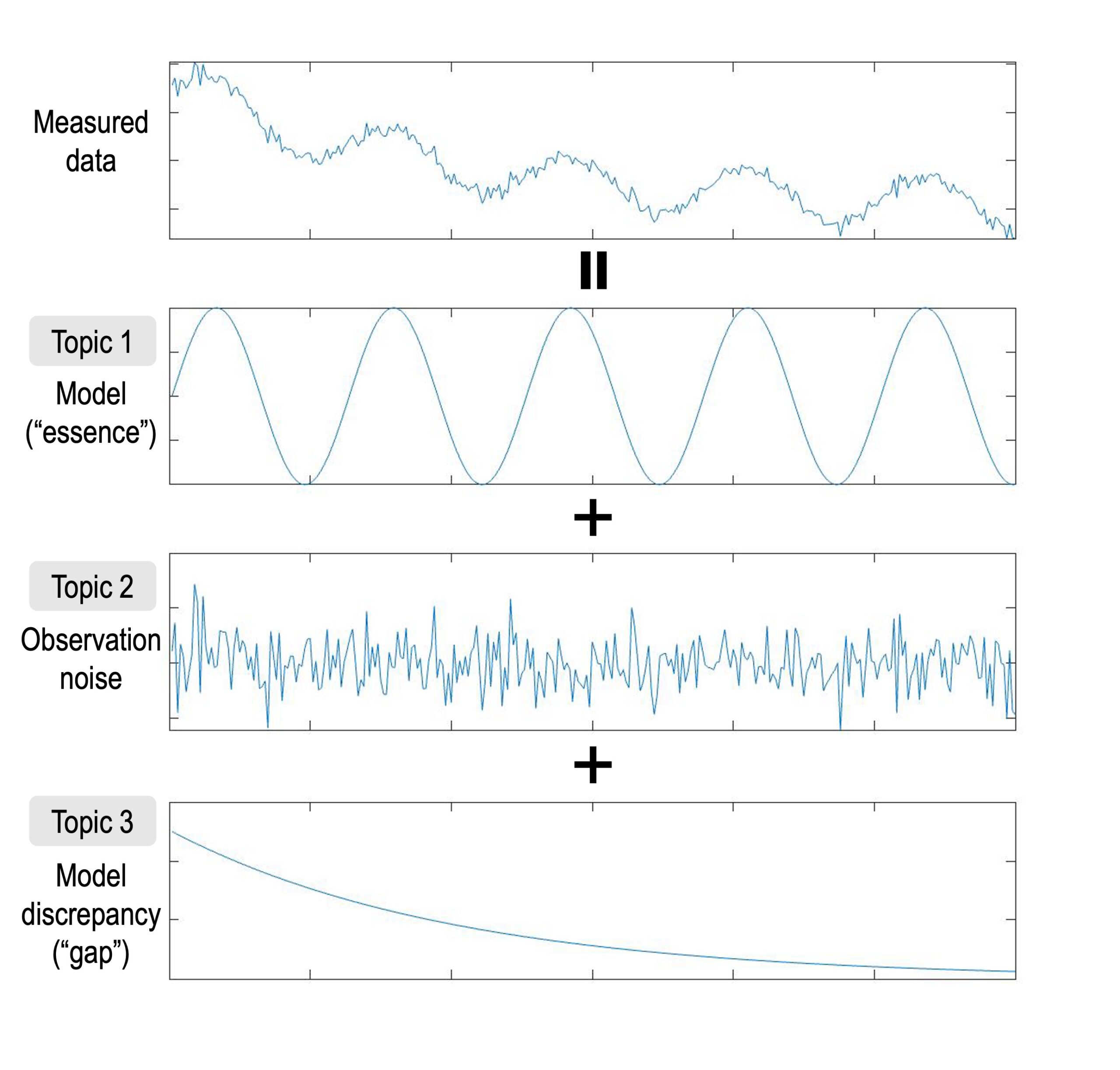
While models represent the essence of a phenomenon, what that essence is is not self-evident. This judgment is left to the researcher’s insight, and there may be differences of opinion among researchers. For example, an oscillatory phenomenon can be modeled as a sinusoid if the friction is negligible or as a damped sinusoid if the friction is considerable. We conduct empirical research to resolve such indefiniteness using Bayesian statistics, which quantifies the validity of each model for a given dataset as a probability. We have demonstrated the usefulness of Bayesian statistics in selecting models for condensed matter physics, such as velocity distribution functions and band structures. We also study the mathematical mechanisms underlying this Bayesian methodology.

Topic 2: Effects of observation noise

Measured data is always contaminated by observation noise, and the larger the noise, the more uncertain the parameter values estimated from the data become. We have focused on the fact that the nature of error propagation also affects model selection and have developed a methodology for jointly estimating noise variance and a valid model. We have also demonstrated the usefulness of this methodology through some examples in our empirical research. Estimating parameters and models depends on the quantity and quality of data. We have pioneered an asymptotic theory of Bayesian inference that considers the effects of noise by advancing theoretical analysis based on the mathematical correspondence between Bayesian statistics and the statistical mechanics of disordered systems. We are currently working on extending the theory to various types of noise that appear in measurements.

Topic 3: Effects of model discrepancy

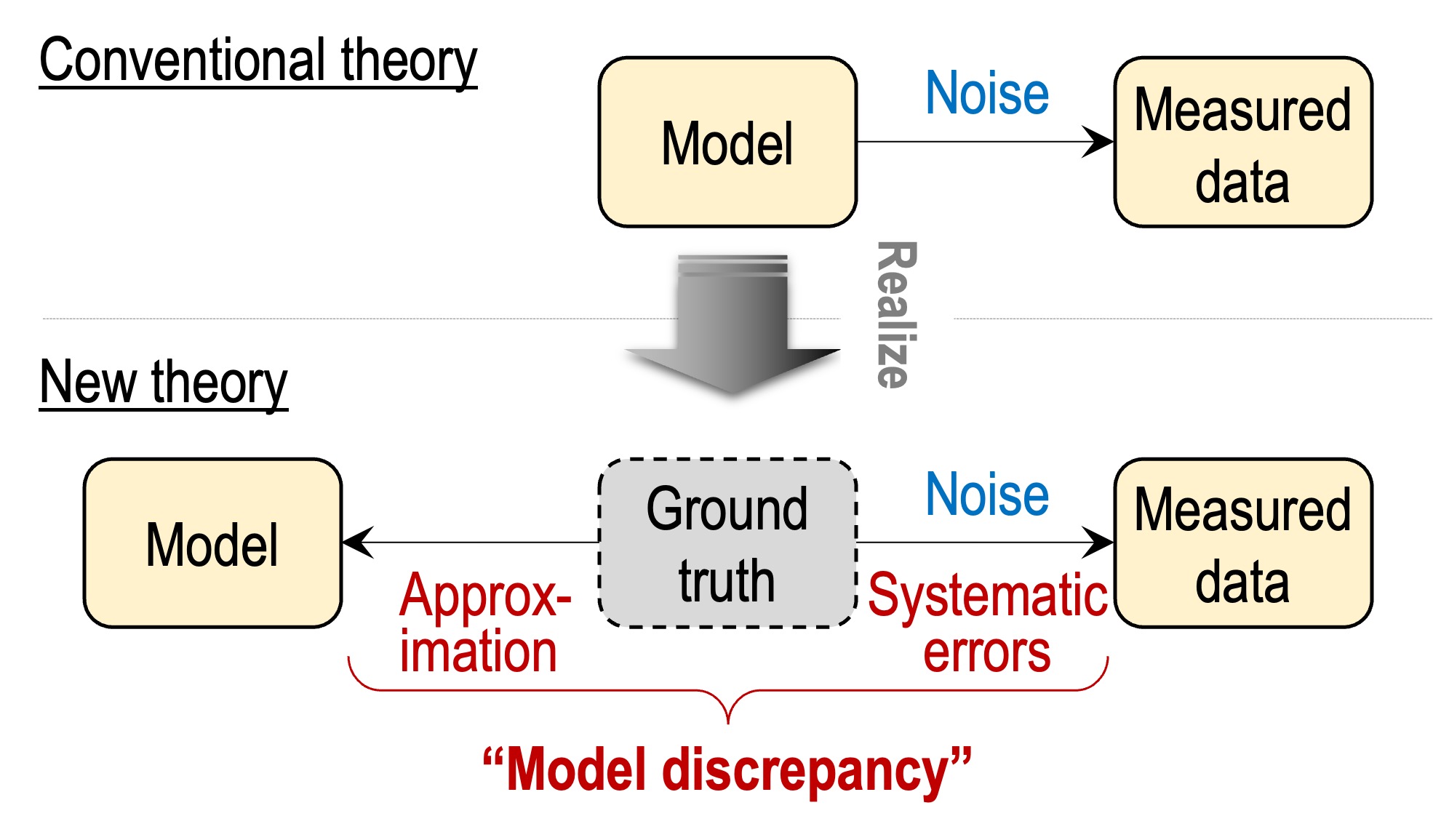
There is always a gap between ideals and reality, i.e., between models and measured data. A model is just an approximate representation of ground truth, and there are also observational noise and systematic errors between the ground truth and the measured data. We refer to all the above together, but random noise, as the model discrepancy. Attributing the origins of the model discrepancy is difficult, and describing them in a simple mathematical expression is even more difficult. Besides, the conventional asymptotic theory of Bayesian inference is based on the assumption that model discrepancy does not exist. We are exploring systematic ways to address model discrepancy and developing a theory to support their validity.

Collaborators

• Group of Physical Materials Modeling and Machine Learning, Future University Hakodate
• Photoemission Solid-State Physics Lab., Tohoku University
• Mathematics for Advanced Materials Open Innovation Laboratory (MathAM-OIL), AIST
• Plasma and Fusion Physical Science Laboratory, Kyushu University

Projects

• Innovation in a guiding principle for modeling based on observed data (PREST [Measurement and Analysis Foundation], JST）