研究内容

モデリング原理の確立に向けた挑戦

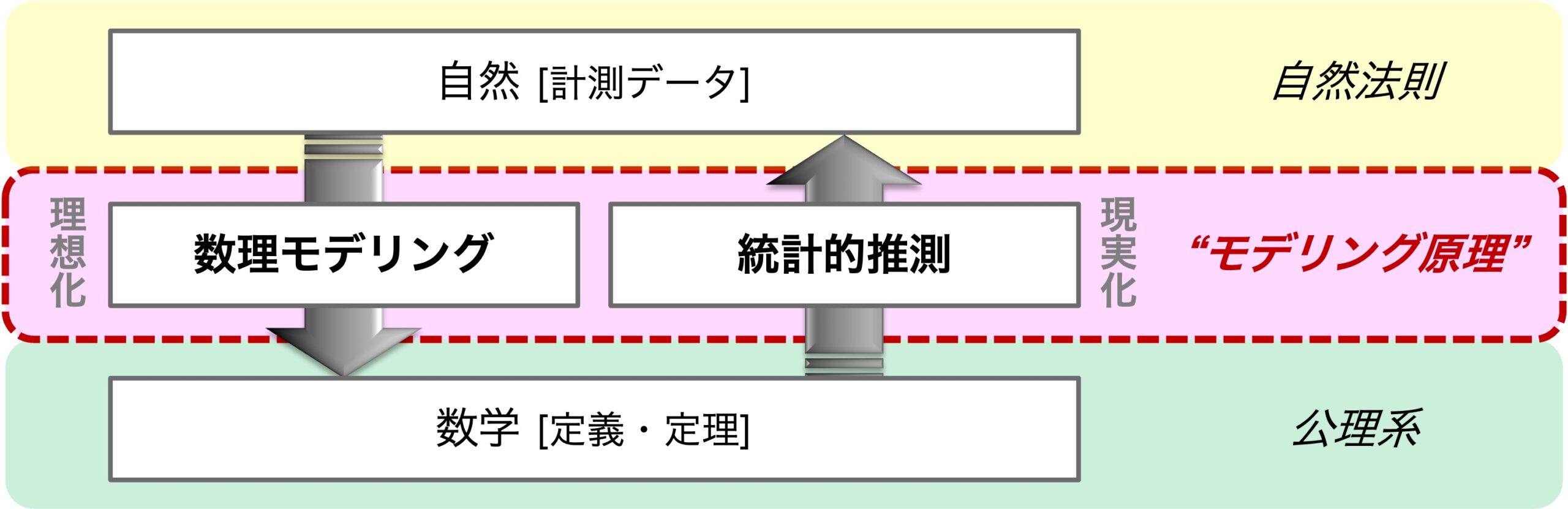
当研究室では数理モデリングと統計的推測を両輪として、あらゆる物理現象を曖昧さなく理解するための指導原理を確立すべく、理論と実証の両面から研究を推進しています。自然と数学はそれぞれ異なるルール、すなわち自然法則と公理系の下で個別に成り立つ世界です。数理モデリングはこれらの世界をつなぐ手段の一つであり、単純な数式を用いて計測データを表すことで、現象が有する普遍性と個別性を切り分けて理解する足掛かりを築きます。ただし、モデルは自然の一部を数学的に扱うために理想化した表現であり、現実の自然そのものではありません。統計的推測はモデルをより現実に近づける手段の一つであり、計測データとの定量的照合を通じて、実態に即したモデルを複数の候補の中から選択し、そのパラメータの推定を可能にします。数理モデリングと統計的推測を組み合わせることで、自然と数学、すなわち現実と理想の間の行き来が実現します。

数学の精緻な理論体系に比べて、数理モデリングの指導原理は十分に明確化（公理化）されておらず、その曖昧さが現象の解釈に際して論争を生むこともあります。加えて、統計的推測は必ずしも各分野における数理モデリングの設計思想を反映した結果を導かず、”X学的な妥当性”（X = 物理, 化学, 生物, …）の統計学的な定式化・定量化が求められています。我々は“モデリング原理”とも呼ぶべき、数理モデリングと統計的推測にまたがる統一ルールを確立し、以下の2つの相補的なアプローチを一貫して実現する学問体系を築くことを目指しています。

1. 統計的推測を視野に入れた数理モデリング
2. 数理モデリングの設計思想を反映した統計的推測

研究課題１：モデルの不定性

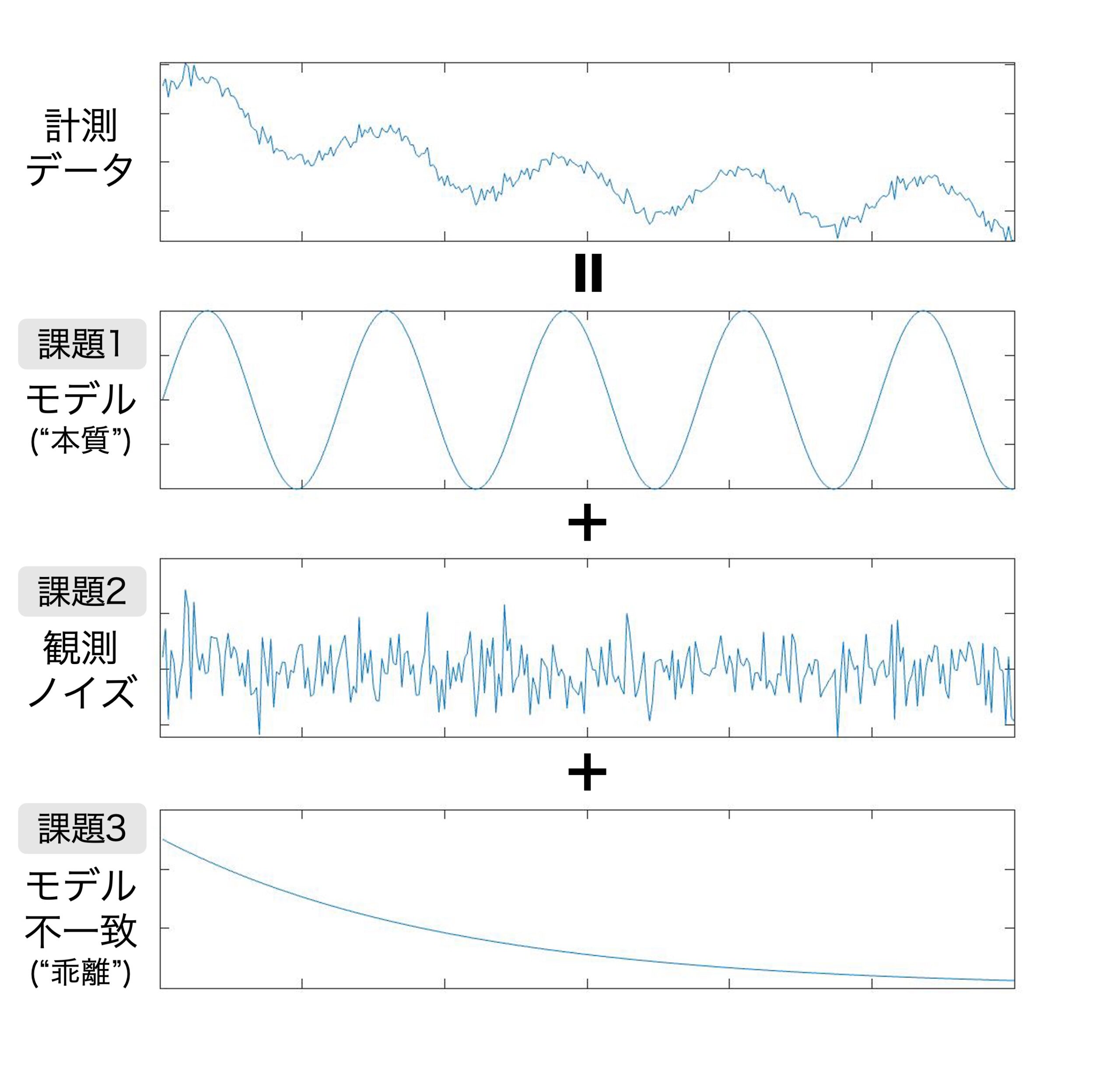
モデルは現象の本質を表す一方、何が本質かは自明ではありません。その判断は研究者の洞察に委ねられ、研究者間で見解の相違が生じることもあります。例えば、図の計測データが示す振動現象は摩擦が無視できるならば単振動、そうでなければ減衰振動としてモデリングできますが、どちらが妥当であるかは場合によります。我々はデータに対する各モデルの妥当性を確率として定量化するベイズ統計に則り、こうした不定性を解消する実証研究を進めています。これまでの成果として、速度分布関数やバンド構造など、凝縮系物理学におけるモデルの選択に対してその有用性を示してきました。このようなベイズ統計に基づく方法論に潜む数理的機構を解明し、方法論に理論保証を与える研究も併せて進めています。

研究課題２：観測ノイズの影響

計測データには必ず観測ノイズが伴い、観測ノイズが大きいほど、データから推定するパラメータの値も不確実になります。我々はこうした誤差伝搬の性質がモデルの評価にも影響することに着目し、ノイズ分散と妥当なモデルを同時推定する方法論を開発しました。これまでの成果として、いくつかの実証研究を通じてその有用性を示してきました。パラメータやモデルの推定はデータの量や質に依存します。我々はベイズ統計と不規則系の統計力学の数学的対応に立脚した理論解析を進めることで、ノイズの影響を考慮したベイズ推定の漸近理論を開拓しました。現在、計測に現れる様々なタイプのノイズに理論を拡張すべく、研究を進めています。

研究課題３：モデル不一致の影響

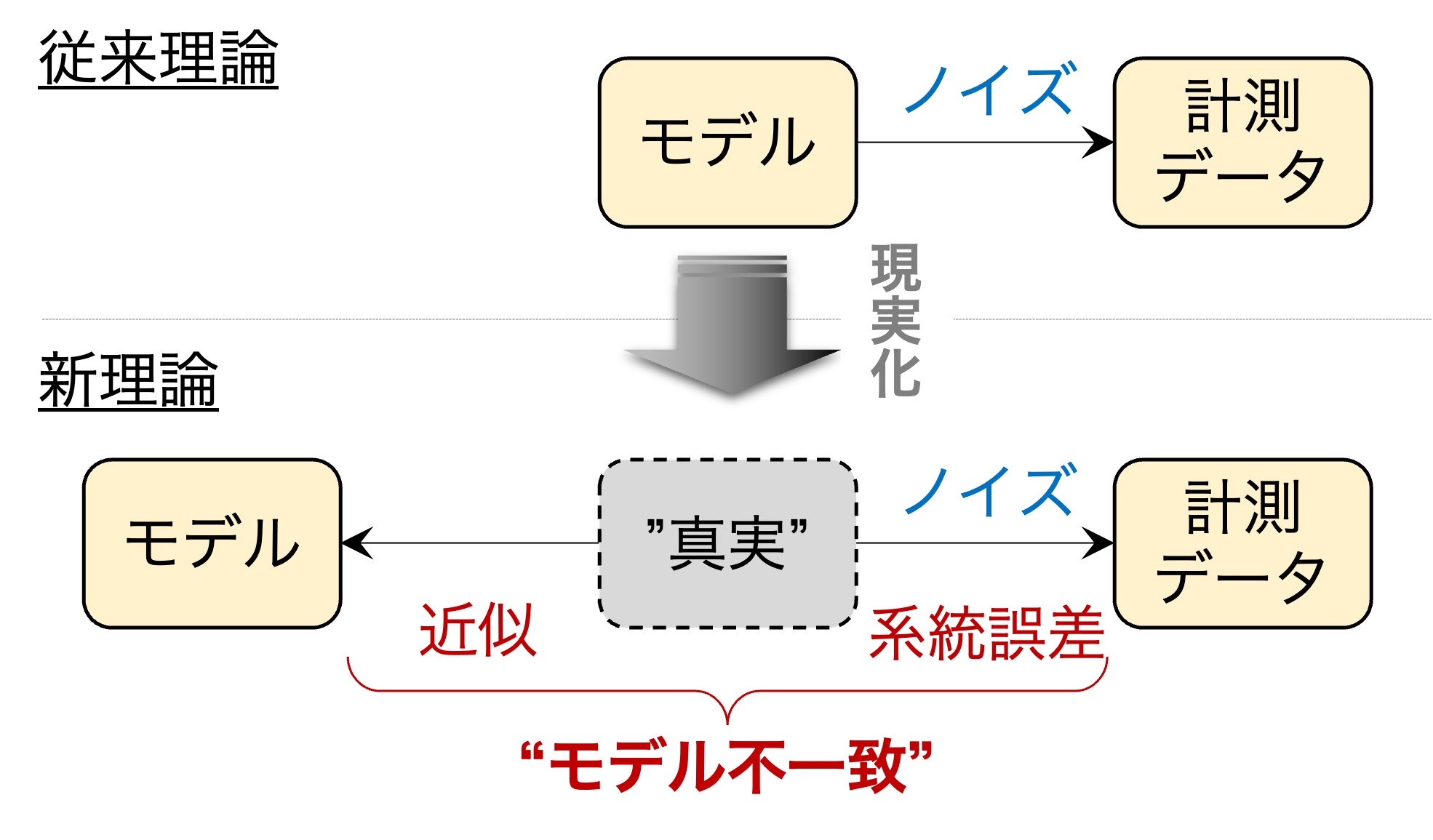
理想と現実、すなわちモデルと計測データの間には常に乖離があります。モデルはあくまで真実の近似であり、真実と計測データの間には観測ノイズや系統誤差が存在します。我々はこれらの内、ランダムな観測ノイズ以外をまとめてモデル不一致と総称します。モデル不一致の起源を帰属することは容易でなく、それらを単純な数式で表すことはさらに困難です。また、ベイズ推定の漸近理論（従来理論）はモデル不一致のない状況を仮定します。我々はモデル不一致への系統的な対処法を探求し、その正当性を裏付ける新理論の構築に挑んでいます。

主な共同研究先

• 公立はこだて未来大学 情報システム学部 義永グループ
• 東北大学 材料科学高等研究所(AIMR) 佐藤研究室
• 産業技術総合研究所 数理先端材料モデリング オープンイノベーションラボラトリ(MathAM-OIL)
• 東京大学 大学院新領域創成科学研究科 岡田研究室
• 九州大学 応用力学研究所 核融合プラズマ理工学研究室

進行中のプロジェクト

• 計測データに根ざしたモデリング原理の革新 (JSTさきがけ「計測解析基盤」領域)